Over the centuries, the history of mathematics has witnessed the rise of many greats: Pythagoras, Thales, Newton, Archimedes.
But what did Euclid discover? Often called the Father of Geometry, Euclid lived around 300 BCE and made one of the most lasting contributions in all of math: the Euclidean algorithm, a method still used today to find the greatest common divisor.
Euclid helped shape the foundation of modern mathematics. But instead of creating new theories, he organized and refined existing knowledge into Elements — a text that shaped centuries of learning.
Today, his work remains evident in everything from school lessons to advanced topics, such as the Euclidean distance formula in data science. Let’s dive into Euclid’s life, his discoveries, how he inspired some of the most famous mathematicians in history and why his thinking still matters.

The Euclidean Algorithm
One of Euclid’s most lasting contributions is the Euclidean algorithm — a method that makes it possible to find the greatest common divisor (GCD) of two integers. First introduced in Book VII of Elements, this technique relies on repeated division or subtraction until only a remainder of zero remains.
Take, for example, the numbers 48 and 18:
- Divide 48 by 18 → quotient 2, remainder 12
- Divide 18 by 12 → quotient 1, remainder 6
- Divide 12 by 6 → quotient 2, remainder 0
Since there’s no remainder, the GCD of 48 and 18 is 6.
This simple yet powerful process, now known as Euclid’s algorithm, remains a cornerstone of number theory and plays a vital role in everything from cryptography to basic arithmetic lessons.
Not sure how to use it correctly? A math tutor near you can help you work through step-by-step examples and gain confidence using this timeless technique.
The Euclidean algorithm is over 2,000 years old and is still one of the most efficient ways to compute the GCD, even in modern programming.
Euclidean Distance Formula
While Euclid is best known for his contributions to arithmetic, his legacy in geometry is just as profound. His work in Elements laid the foundation for what we now call Euclidean geometry — the system of geometric principles still taught in schools today.
One of the most widely used tools that evolved from this system is the Euclidean distance formula, which calculates the shortest path between two points in space. For any two points, (x₁, y₁) and (x₂, y₂), the formula looks like this:
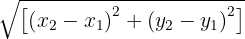
This method of measuring Euclidean distance may appear simple, but it’s a core concept in many fields — from classical geometry to modern applications like computer graphics, GPS mapping, and machine learning.
Although Euclid didn’t write this formula in its modern form, it stems directly from the geometric logic and principles outlined in his seminal text. If visualizing two-dimensional and three-dimensional space feels abstract, working with a qualified math tutor online can help you connect theory with real-world understanding.
Here's a 2 minute tutorial to help you get started 👇

Euclid’s Algorithm vs Euclidean Distance
Although they sound similar, Euclid’s algorithm and the Euclidean distance formula serve different mathematical purposes. Their shared origin lies in Elements, but their applications stretch across completely different fields.
Euclid’s algorithm is a step-by-step method for finding the greatest common divisor (GCD) of two numbers using repeated division or subtraction. It’s a foundational concept in number theory and plays a vital role in areas like cryptography and simplifying fractions.
On the other hand, the Euclidean distance formula calculates the straight-line distance between two points in a plane or space. It stems from geometric principles and is used widely in disciplines like physics, machine learning, and computer graphics.
To help clarify the distinction, here’s a side-by-side comparison:
| Feature | Euclid’s Algorithm | Euclidean Distance Formula |
|---|---|---|
| Purpose | Finds the greatest common divisor (GCD) | Measures straight-line distance between points |
| Field | Number theory | Geometry, spatial analysis |
| Mathematical Process | Repeated division or subtraction | Square roots and coordinate subtraction |
| First Described In | Elements, Book VII | Derived from Elements, via geometric principle |
| Real-World Use | Cryptography, simplifying fractions, coding theory | Machine learning, physics, and computer graphics |
Despite the name overlap, the two highlight how Euclid’s contributions stretched across multiple mathematical domains. His legacy aligns with that of other monumental figures like Sir Isaac Newton, who similarly bridged abstract theory with real-world application in both physics and mathematics.
Euclid’s Light Theory and Contributions to Optics
Euclid wasn’t only concerned with numbers and geometry — he also explored the nature of light and visual perception.
In his lesser-known treatise Optics, Euclid proposed one of the earliest theories about how we see the world.
This idea, now known as the Euclid light theory, suggested that vision operates through rays emitted in straight lines from the eyes, interacting with the environment to create perception. Although modern science has reversed this idea (we now understand that light enters the eye), Euclid’s attempt to explain sight using geometry was a groundbreaking step for both physics and mathematics.
By applying what we now call Euclidean principles to optics, Euclid examined how angles, lines, and distances shape what we see, including the behavior of reflections and the perceived size of objects at varying distances. His structured, logical approach to understanding the natural world turned vision into a mathematical study, much like he did for geometry in his legendary work Elements.
His contributions in this area are part of a larger tradition of thinkers who bridged disciplines, such as Archimedes, who applied mathematics to physics and engineering in revolutionary ways. Just as Archimedes transformed our understanding of volume and force, Euclid gave structure to how we interpret space and light.

What makes Euclid’s work especially remarkable is that he was developing Optics while simultaneously composing Elements, a thirteen-book volume that continues to underpin modern geometry and arithmetic.
The first six books in Elements deal with the geometric plane. The second book is dedicated to irrational quantities. It is comprised of the three last books, which are devoted to geometry in space. Here, we see the construction of objects like the sphere, regular solids, the pyramid, the cube, the octahedron, the dodecahedron, the icosahedron, etc. Other books have been grafted onto Elements during the course of its centuries long.
His capacity to link seemingly unrelated domains like light and numbers speaks to the power of a Euclidean worldview: one where logic, structure, and clarity shape our understanding of everything from triangles to telescopes.
These early ideas didn’t vanish with time. They were carried through the Islamic Golden Age and resurfaced during the European Renaissance, informing the work of later mathematicians and philosophers. For instance, René Descartes would build on Euclid’s framework to develop analytic geometry and explore how vision, math, and reason intertwine.
Other Discoveries by Euclid
Euclid’s name is most often associated with geometry and his iconic Elements, but his impact stretches far beyond a single theorem or diagram. From fundamental arithmetic to 3D geometry, his systematic thinking shaped the entire framework of how math is studied and taught today.

Want to learn about other ground-breaking mathematicians, read about Pythagoras!
What is Euclidean Division?
In the section of coursework and curriculum dedicated to arithmetic, Euclidean division is certainly one of the mathematical skills that is still taught from antiquity. It is nothing more than the division that one learns in elementary school. Also called whole division, it is composed of an operation between two whole numbers called a dividend and a divisor, which gives the results called the quotient and the remainder. Making a Euclidean division of one number A (the dividend) by one number B (the divisor), permits us to try to find a whole quotient. That is to say, the whole integer found at the end of the division is called the remainder, which is the part of the dividend that we cannot divide further. To better understand, here’s an example: With the dividend of 25, we divide by 4 (the divisor). The quotient turns out to be 6 because 6 X 4 =24. What is left over is 1. The number 1, then, is the remainder. The common way to write this type of division is to place the dividend on the left side and the divisor on the right. The remainder is found under the dividend while the quotient is found under the divisor. To verify that you have finished the operation, make sure that the remainder cannot be divided further. It will be necessarily smaller than the divisor. It could be that the remainder is zero. In this case, we say that A is a multiple of B. Euclidean division is an integral part of our elementary courses, although this division can and does get more complicated with the addition of decimals, etc. Find Waterloo math courses with a tutor from Superprof.
Euclid's Mathematical Axioms
In his work Elements Euclid wrote many axioms, which are mathematical propositions that are held as evident. It was at this moment in history that the mathematical world decided to designate name “axiom” to all mathematical rules that were at once elementary and logical. Euclid gave 5 in his work:
- “A straight line segment can be drawn joining any two points.
- “Any straight line segment can be extended indefinitely in a straight line.
- “Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
- “All right angles are congruent.
















